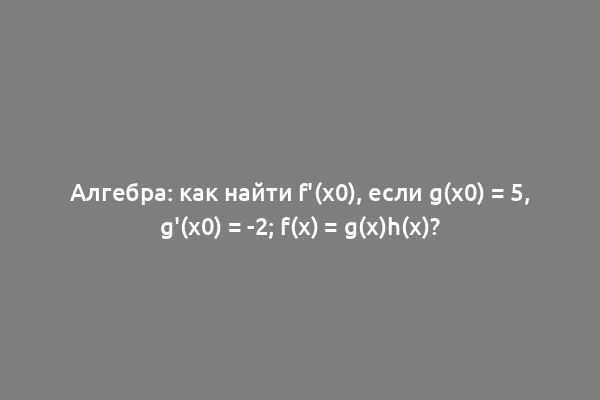g(x0) = 5, g'(x0) = -2;
h(x0) = 2,h'(x0) = 0,4;
f(x) = g(x)h(x).
Вычислите f'(x0).
тэги:
алгебра,
задача,
математика,
школа,
школьная программа,
школьные знания
категория:
образование
ответить
комментировать
бонус
1 ответ:
старые выше
новые выше
по рейтингу
0
Mefody66
[42.5K]
2 месяца назад
Нам дано:
g(x0) = 5, g'(x0) = -2;
h(x0) = 2,h'(x0) = 0,4;
Нам известно, что:
f(x) = g(x)h(x).
Значит, f(x0) = g(x0)*h(x0) = 5*2 = 10
Берем производную от f(x) по правилу производной от произведения:
f'(x) = g'(x)*h(x) + g(x)*h'(x)
Подставляем x0:
f'(x0) = g'(x0)*h(x0) + g(x0)*h'(x0) = -2*2 + 5*0,4 = -4 + 2 = -2
Ответ: -2
Источник: